Go Back

算法设计与分析

学习笔记

选择题10道，20分

填空题20道，30分


简答题3道，30分


文件上传题2道，20分


考试成绩占比60%

第一章

算法的渐进复杂性（5个）

渐进复杂性的性质（5个）

循环的时间复杂度

NP问题

第二章

递归

直接或间接地调用自身地算法称为递归算法。用函数自身给出定义的函数称为递归调用。

递归例子

  1. 阶乘函数

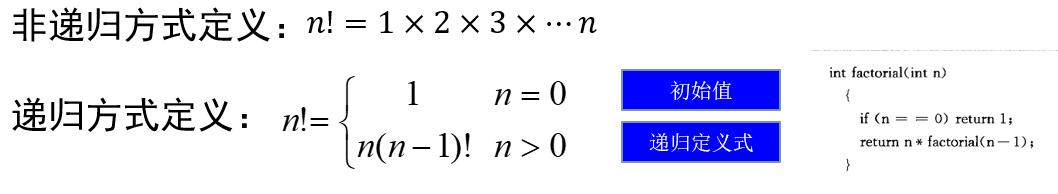
    202404211835407.png

    每个递归函数，必须有非递归定义的初始值，否则无法进行递归计算

  2. Fibonacci数列

    无穷数列1，1，2，3，5，8，13，21，···

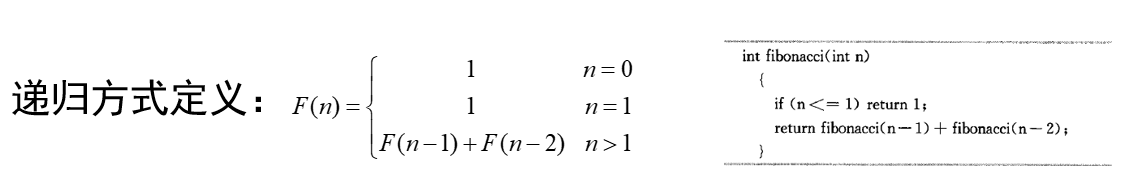
    202404211842736.png

  3. 全排列

    def permute(a, l, r, result):
    if l==r:
        result.append(''.join(a))
    else:
        for i in range(l,r+1):
            if shouldSwap(a, l, i):
                a[l], a[i] = a[i], a[l]
                permute(a, l+1, r, result)
                a[l], a[i] = a[i], a[l]
​
def shouldSwap(a, start, curr):
    for i in range(start, curr):
        if a[i] == a[curr]:
            return 0
    return 1

  4. 整数划分

    将正整数n表示成一系列正整数之和

    202404212056675.png

  5. 汉诺塔

    202404212106559.png

递归小结

优点

  • 结构清晰、可读性强
  • 容易用数学归纳法来证明算法正确性，为设计算法、调试程序带来很大方便

缺点

  • 运行效率低，耗费的计算时间和占用的存储空间都比非递归算法多

解决方法：在递归算法中消除递归调用，使其转化为非递归算法

  • 采用一个用户定义的栈来模拟系统的递归调用工作栈。本质上还是递归，根据具体的程序对递归调用工作栈进行简化，减少栈的操作，压缩栈的空间
  • 用递推实现递归函数
  • 通过变换将一些递归转化为尾递归（从最后开始计算，每递归一次就算出相应的结果）

分治算法

四个性质

  • 该问题的规模缩小到一定的程度就可以容易地解决
  • 可以分解为若干个规模较小的相同问题，即具有最优子结构性质
  • 利用该问题分解出地子问题地解可以合并为该问题的解（完全取决于这条特征，若只满足前两条则可考虑贪心算法或动态规划）
  • 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题（与效率有关）

解决问题思路

202404212121278.png

时间复杂度

202404212122945.png

例子

二分搜索

开始时，先找出有序集合中间的那个元素。如果此元素比要查找的元素大，就接着在较小的一个半区进行查找；反之，如果此元素比要找的元素小，就在较大的一个半区进行查找。在每个更小的数据集中重复这分析：如果n=1即只有一个元素，则只要比较这个元素和x就可以确定x是否在表中。

时间复杂度计算：共n个元素，第一次查找的区间是n，第二次查找的区间是n/2，第三次是n/4，直到第k次，n/2k-1。设第k次，只剩下1个元素，不需要再进行搜寻，即n/2k-1=1，k-1 = log2n，即k= log2n+1，化简为k= log2n。每次耗费的时间均为单位时间O(1)，所以，时间复杂性为O(logn)

202404212249599.png

大整数乘法

202404251948991.png

合并排序（MergeSort)

void MergeSort(Type a[], int left, int right)
   {
      if (left<right) {//至少有2个元素
      int i=(left+right)/2;  //取中点
      mergeSort(a, left, i);
      mergeSort(a, i+1, right);
      merge(a, b, left, i, right);  //合并到数组b
      copy(a, b, left, right);    //复制回数组a
      }
   }

Merge和Copy可以在O(n)时间内完成。

202404251956756.png

自然合并排序是上述合并排序算法MergeSort的一个变形，在上述合并排序算法中,第一步合并相邻长度为1的子数组段,这是因为长度为1的子数组段是已排好序的。事实上,对于初始给定的数组a,通常存在多个长度大于1的已自然排好序的子数组段例如,若数组a中元素为{4,8,3,7,1,5,6,2},则自然排好序的子数组段有{4,8},{3,7},{1,5,6}和{2}。（5，6是相邻有序的，所以划分在一起）

202404252035411.png

快速排序

①选择A中的任意一个元素pivot（支点），该元素作为基准

②将小于基准的元素移到左边，大于基准的元素移到右边（分区操作

③A被pivot分为两部分，继续对剩下的两部分做同样的处理

④直到所有子集元素不再需要进行上述步骤

template<class Type>
void QuickSort (Type a[], int p, int r)
{
      if (p<r) {
        int q=Partition(a,p,r); 确定分段位置
        QuickSort (a,p,q-1); //对左半段排序
        QuickSort (a,q+1,r); //对右半段排序
        }
}

优点：在快速排序中，记录的比较和交换是从两端向中间进行的，关键字较大的记录一次就能交换到后面单元，关键字较小的记录一次就能交换到前面单元，记录每次移动的距离较大，因而总的比较和移动次数较少。

202404252052208.png

202404252052586.png

快速排序算法性能取决于划分的对称性，取决于基准元素的选择。

  • 第一个或最后一个：如果待排序数据已经排好序的，就会产生一个很糟糕的分割。几乎所有的数据都被分割到一个集合中，而另一个集合没有数据。这样的情况下，时间花费了，却没有做太多实事。而它的时间复杂度就是最差的情况O(N2)。因此这种策略是绝对不推荐的。
  • 随机选择：随机选择基准是一种比较安全的做法。因为它不会总是产生劣质的分割。
  • 选择三数中值：如果能够选择到数据的中值，那是最好的，因为它能够将集合近乎等分为二。但是很多时候很难算出中值，并且会耗费计算时间。可随机选取三个元素，用它们的中值作为整个数据中值的估计值。

快速排序与合并排序相比

快速排序：常用，算法效率不太稳定

合并排序：稳定，但额外内存空间占用多

线性时间选择

给定线性序集中n个元素和一个整数k，1≤k≤n，要求找出这n个元素中第k小的元素，即如果将这n个元素线性排序（升序），则排在第k个位置的元素为要找的元素。当k=1时，最小元素，k=n，最大的元素，k=(n+1)/2时，为中位数。

方法一

先排序，再寻找，寻找时间为O（n）

方法二

借鉴快速排序算法，对其中一段持续分解，最坏的情况为O(n2)，平均时间为O(n) （1）利用随机快速排序算法，随机选取基准数，将目标数组分为两组，其中前一个小组中的元素均不大于后一个小组的元素。计算前面小组的元素个数j， （2）若k<=j，则在前面的子数组中寻找第k个元素 （3）若k>j，则需要在后一个子数组中进行寻找，其位置为k-j。 最坏的情况：在寻找最小元素的时候，总是在最大元素处划分。 T(n) = T(n-1)+O(n)

方法三

改进快速排序算法，时间为O(n)

202404252131016.png

202404252131620.png

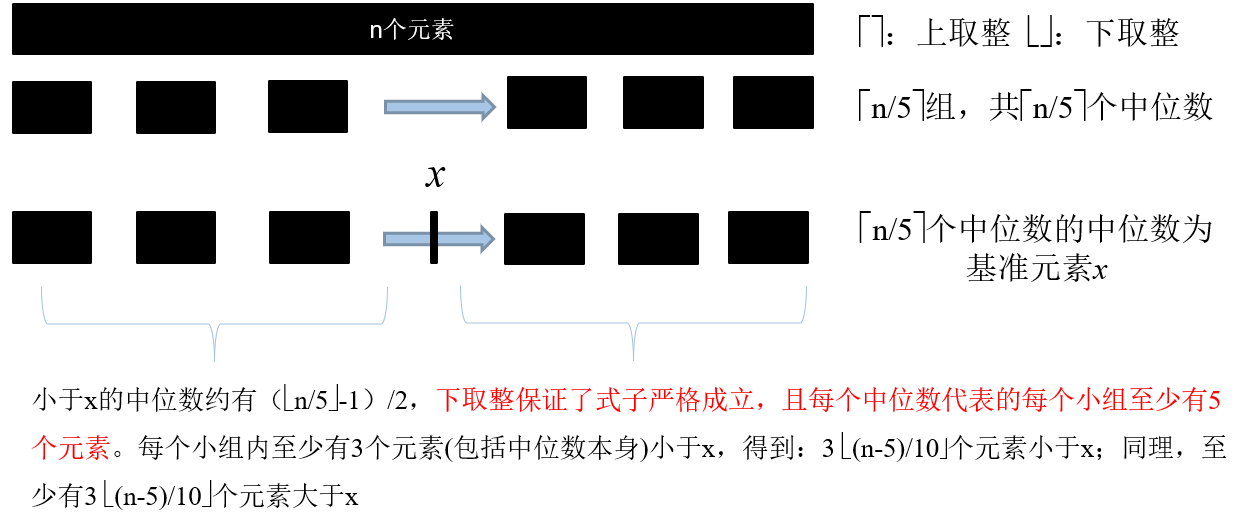
202404252132326.png

202404252132224.png

202404252132970.png

最接近点对问题（一维二维，处理问题过程，推导，划分，候选点）

给定平面上n个点的集合S，找其中的一对点，使得在n个点组成的所有点对中，该点对间的距离最小。

什么是平衡子问题

主定理公式

动态规划

两个性质

如何用它解决问题

七个例子（矩阵连乘（递归公式，自底向上），最长公共子序列（ci公式，cij，bij表格，公共子序列，追踪解），最大子段和（分治法和动态规划解决，解决顺序），图像压缩（过程，l，b，s，），流水作业问题（只考两台机器，T(s,t)的理解，johnsn不等式），0-1背包问题（填表，追踪解过程），最优二叉搜索树（带权路径和，关键字伪关键字，递归公式））

贪心选择算法

两个性质

5个例子（活动安排问题（策略（结束早的优先））背包问题（按单位重量价值排序，大的优先），最优装载问题（重量轻的优先），哈夫曼编码（前缀码，平均传输位数，二叉树（左0右1）），单源最短路径（有向带权，Dijkstra算法 表格），最小生成树（无向带权，prim算法，？算法））

备忘录方法 与动态规划区别